렐루(ReLU)와 같은 활성화 함수는 모델의 비선형성을 증가시키기 위해서 신경망의 중간 (은닉)층에 주로 사용된다.
시그모이드(이진 분류)나 소프트맥스(다중 분류)같은 함수는 마지막 출력층에 추가되어 클래스 소속 확률을 출력한다.
시그모이드와 소프트맥스 활성화 함수가 출력에 포함되지 않으면 모델은 클래스 소속 확률대신 로짓(logit)을 출력하는 것임
Loss function
분류 문제에 초점을 맞추면 문제의 종류(이진 분류, 다중 분류)와 출력의 형태(로짓, 확률)에 따라 모델 훈련에 필요한 적절한 손실 함수를 선택해야 한다.
이진 크로스 엔트로피(Binary cross-entropy)는 (하나의 출력 유닛을 가진)이진 분류를 위한 손실 함수이다.
범주형 크로스 엔트로피(Categorical cross-entropy)는 다중 분류를 위한 손실 함수이다.
희소한 범주형 크로스 엔트로피(Sparse categorical cross-entropy)는 범주형 크로스 엔트로피가 원-핫 인코딩 레이블일 경우
원-핫 인코딩에 대한 레이블을 출력한다면, 희소한 범주형 크로스 엔트로피는 정수 정답 레이블에 대해 출력한다.

Entropy
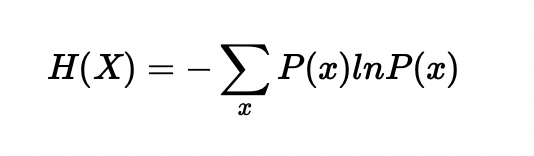
Cross-Entropy, CE
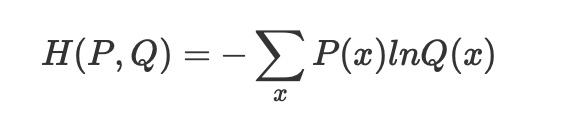
CE, E의 차이는 실제값p와 타깃이 되는 예측값q의 정보량 비율 합으로 구해진다.
Binary Cross Entropy Error, BCEE & Categorical Cross Entropy Error, CCEE

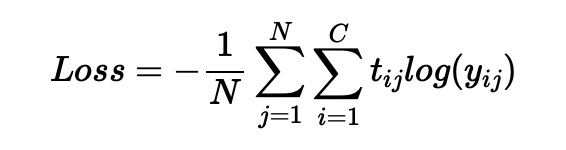
CE의 평균이 BCEE, CCEE이다.
클래스 소속 확률보다는 로짓으로 크로스 엔트로피 손실을 계산하는 것이 수치상의 안정성 때문에 일반적으로 선호된다.
손실 함수의 입력으로 로짓을 사용하고, from_logits=True로 지정하면 해당하는 텐서플로 함수는 훨씬 효율적으로 구현을 사용하여
손실과 가중치에 대한 손실의 도함수를 계산한다.
로짓이 입력으로 제공되면 일부 수학 항을 소거할 수 있어 계산에서 효율적이다.
BCE
import tensorflow as tf
#Binary Cross Entropy
bce_probas=tf.keras.losses.BinaryCrossentropy(from_logits=False)
bce_logits=tf.keras.losses.BinaryCrossentropy(from_logits=True)
logits=tf.constant([0.8])
probas=tf.keras.activations.sigmoid(logits)
tf.print('BCE(확률): {:.4f}'.format(bce_probas(y_true=[1], y_pred=probas)),'(로짓): {:.4f}'.format(bce_logits(y_true=[1], y_pred=logits)))
BCE(확률): 0.3711 (로짓): 0.3711
CCE
#Categorical Cross Entropy
cce_probas=tf.keras.losses.CategoricalCrossentropy(from_logits=False)
cce_logits=tf.keras.losses.CategoricalCrossentropy(from_logits=True)
logits=tf.constant([[1.5, 0.8, 2.1]])
probas=tf.keras.activations.softmax(logits)
tf.print('CCE(확률): {:.4f}'.format(cce_probas(y_true=[[0, 0, 1]], y_pred=probas)), '(로짓): {:.4f}'.format(cce_logits(y_true=[[0, 0, 1]], y_pred=logits)))
CCE(확률): 0.5996 (로짓): 0.5996
SP_CCE
#Sparse Categorical Cross Entropy
sp_cce_probas=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False)
sp_cce_logits=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
tf.print('Sparse CCE(확률): {:.4f}'.format(sp_cce_probas(y_true=[2], y_pred=probas)), '(로짓): {:.4f}'.format(sp_cce_logits(y_true=[2], y_pred=logits)))
Sparse CCE(확률): 0.5996 (로짓): 0.5996